Elliptic curve cryptography

As its name suggests, elliptic curve cryptography (ECC) uses elliptic curves (like the one shown below) to build cryptographic algorithms.  Because of the features of elliptic curves, it is possible to duplicate classical integer-based public key crypto with ECC. 

Doing so also provides a few advantages compared to the integer-based asymmetric cryptography.

Learn Applied Cryptography

Build your applied cryptography and cryptanalysis skills with 13 courses covering hashing, PKI, SSL/TLS, full disk encryption and more.

Start Learning

Building encryption with elliptic curves

Public key cryptography is based on mathematically “hard” problems.  These are mathematical functions that are easy to perform but difficult to reverse.  The problems used in classical asymmetric cryptography are the discrete logarithm problem (exponents are easy, logarithms are hard) and the factoring problem (multiplication is easy, factoring is hard).

Elliptic curve cryptography is based on the fact that certain mathematical operations on elliptic curves are equivalent to mathematical functions on integers:

• Adding two points on an elliptic curve is equivalent to multiplication
• Multiplying two points on an elliptic curve is equivalent to exponentiation

These operations are the same operations used to build classical, integer-based asymmetric cryptography.  This means that it is possible to slightly tweak existing cryptographic algorithms to work with points on an elliptic curve.

For example, Diffie-Hellman is all about exponentiation.  Key exchange is based on the fact that (xa)b=(xb)a=xab.  Due to the fact that logarithms are “hard” (i.e. have complexity that is exponentially related to the length of the exponents), Diffie-Hellman users can publicly exchange xa and xb without fearing that an eavesdropper could learn the values of their private keys a and b.

With elliptic curve cryptography, xa becomes aX, where X is a point on the elliptic curve.  Since point division is equivalent to logarithms, it’s a “hard” problem, making it infeasible to learn a from aX.  Using this relationship, it is possible to build Diffie-Hellman using elliptic curves.

Why use ECC?

ECC is based on the same “hard” problems as classical integer-based public key cryptography.  This means that ECC algorithms will also be breakable when quantum computing makes Shor’s Algorithm usable.

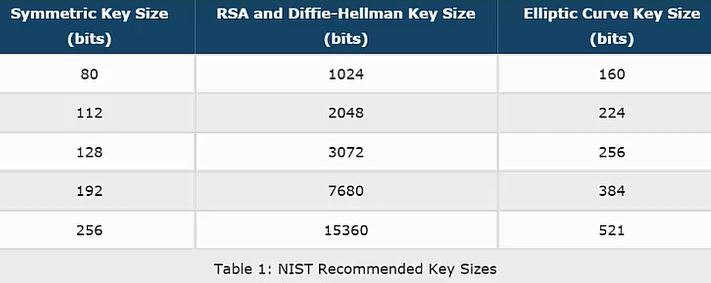
That said, ECC has a couple of advantages over integer-based public key cryptography.  The first of these is key length, as demonstrated in the table below.

This table compares the effective key strength of symmetric cryptography, integer-based public key cryptography, and ECC.  As shown, ECC requires much lower key lengths to achieve the same level of security as RSA and Diffie-Hellman.  While symmetric cryptography needs even shorter key lengths (and is more quantum resistant), it doesn’t have the same functionality as asymmetric cryptography.

This shorter key length makes ECC more efficient than its integer-based counterparts.  An ECC algorithm has lower memory and power requirements than other classical public-key cryptography, making it a better choice for resource-constrained devices like smartphones and Internet of Things (IoT) devices.

Using ECC securely

At the algorithm-level, ECC is as secure as RSA, Diffie-Hellman, and similar algorithms because it is based on the same “hard” problems.  Unless a non-quantum algorithm is found that efficiently solves the factoring or discrete logarithm problems, these algorithms are secure until large enough quantum computers are available.

Where ECC can be complex is curve selection.  A number of different elliptic curves exist, and some are more secure than others.  When implementing ECC, it is important to select a curve that is well-studied and that has no known weaknesses.

Learn Applied Cryptography

Build your applied cryptography and cryptanalysis skills with 13 courses covering hashing, PKI, SSL/TLS, full disk encryption and more.

Start Learning

Conclusion

ECC is an adaption of integer-based classical asymmetric cryptography.  Because it is more efficient in terms of key length and power consumption, it is a useful alternative to integer-based algorithms.

Sources

https://avinetworks.com/glossary/elliptic-curve-cryptography/

https://www.quantiki.org/wiki/shors-factoring-algorithm

https://security.stackexchange.com/questions/200822/if-pgp-is-2048-or-4098-then-what-is-128-bit-encryption